Paradoxical mechanism‍

‍‍I. I. Arto­bolevsky, N. I. Lev­it­sky. Tcheby­shev's Mech­a­nisms / In: P. L. Tcheby­shev’s Sci­en­tific Her­itage. Iss. 2. The­ory of mech­a­nisms. — Moscow-Leningrad: AS USSR. 1945. P. 30–32. (Russ­ian)

‍‍I. I. Arto­bolevsky, N. I. Lev­it­sky. Mod­els of mech­a­nisms of P. L. Tcheby­shev / In: The com­plete works of P. L. Tcheby­shev. Vol. IV. The­ory of mech­a­nisms. — Moscow-Leningrad: AS USSR. 1948. P. 215–217. (Russ­ian)

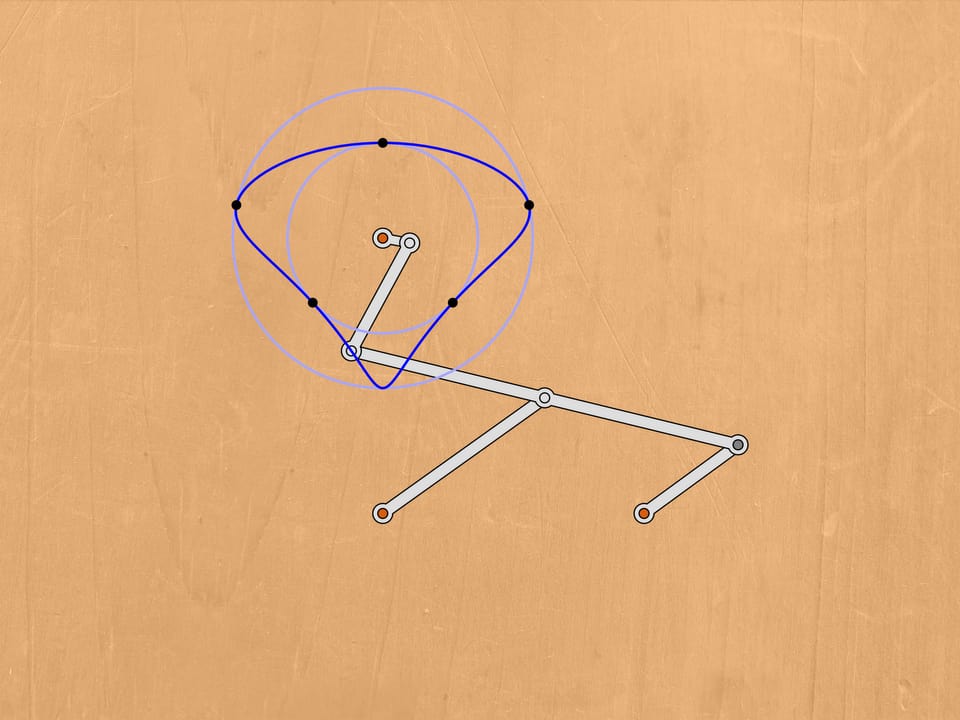
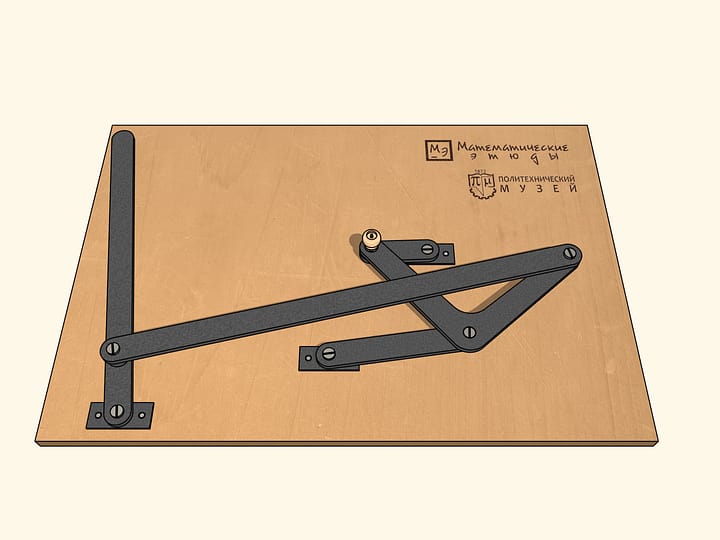
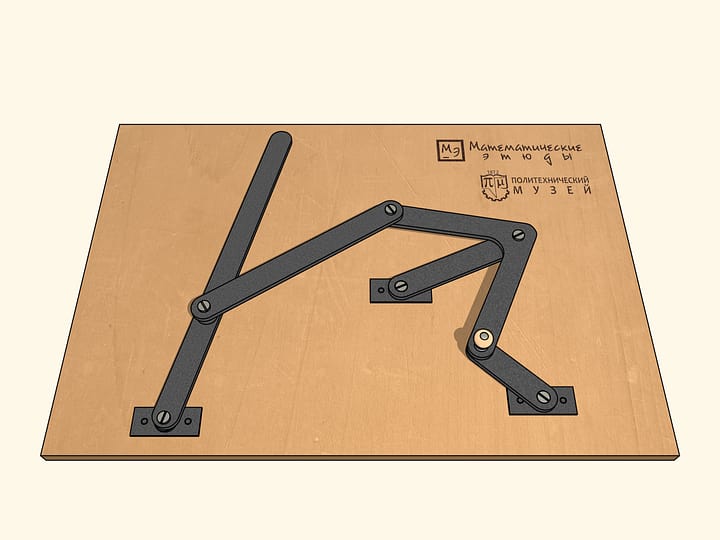
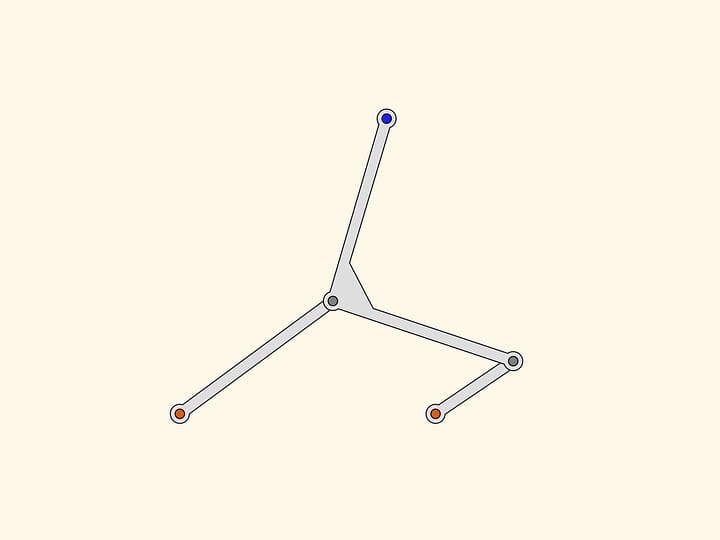
Which trans­for­ma­tion of curves can per­form the given link­age with a sin­gle fixed red hinge?

Let the gray hinge fol­low the curve sym­met­ric with respect to the line pass­ing through the fixed red hinge. One can show that in this case the tra­jec­tory of the blue hinge will also be sym­met­ric with respect to some line pass­ing through the fixed hinge. A russ­ian math­e­mati­cian Pafnuty Lvovich Tcheby­shev inves­ti­gated the ques­tion of this tra­jec­tory.

An impor­tant case of the gray tra­jec­tory is a cir­cle.In prac­tice it's real­ized by adding a fixed (red) hinge and a lead­ing link of some length.

Impor­tant cases of the blue tra­jec­tory are those sim­i­lar to a line seg­ment, a cir­cle or its arc. Tcheby­shev writes: "Here we con­sider the cases that are the sim­plest and most com­mon in prac­tice, that is to obtain motion along a curve, a sig­nif­i­cant part of whom doesn't dif­fer much from a cir­cle arc or a straight line."

Exactly to the ques­tion of find­ing the best para­me­ters of this mech­a­nism, solv­ing prac­ti­cal prob­lems, Pafnuty Lvovich applies for the first time the the­ory of func­tion approx­i­ma­tion, that he devel­oped study­ing the Watt par­al­lel­o­gram.

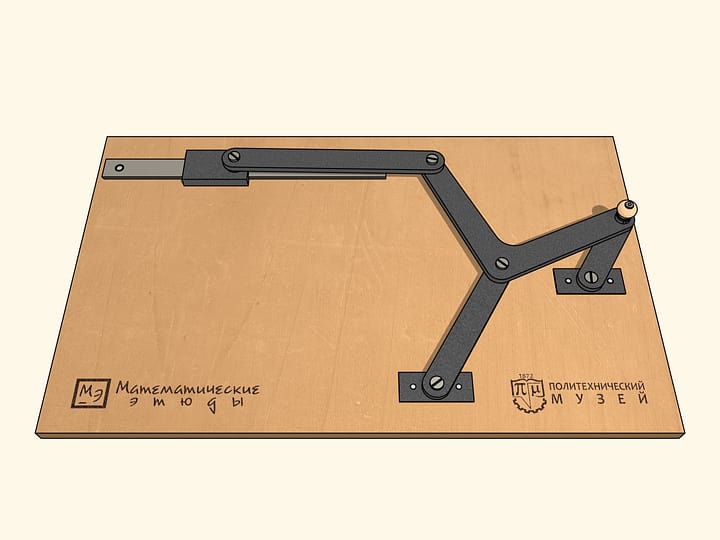
Choos­ing the dis­tance between the fixed hinges, the length of the lead­ing link and the angle between the links, Pafnuty Lvovich obtains a closed tra­jec­tory not dif­fer­ing much from a straight-line seg­ment. The devi­a­tion of the blue tra­jec­tory from a straight one can be decreased chang­ing the para­me­ters of the mech­a­nism. How­ever, the stroke of the blue hinge will decrease as well. But this hap­pens more slowly that the decrease of the devi­a­tion, so one can choose appro­pri­ate para­me­ters for a given appli­ca­tion. This is one of the vari­ants of an approx­i­mate straight­en­ing mech­a­nism pro­posed by Tcheby­shev.

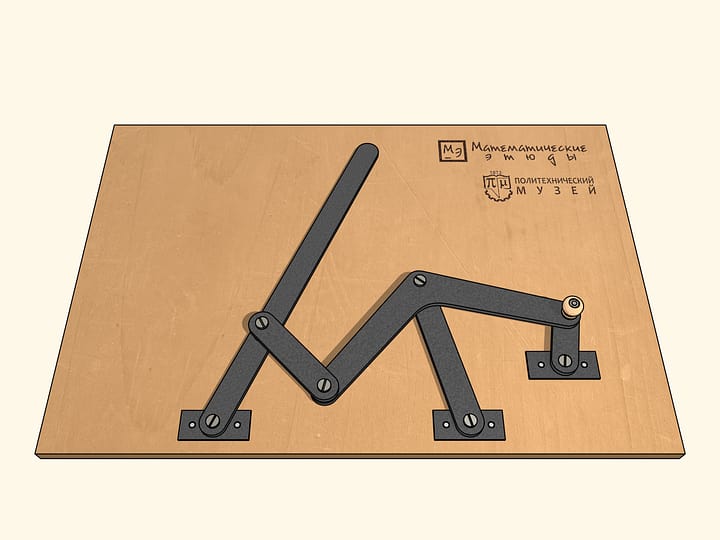
Let's move to the case of sim­i­lar­ity of the blue curve with a cir­cle.

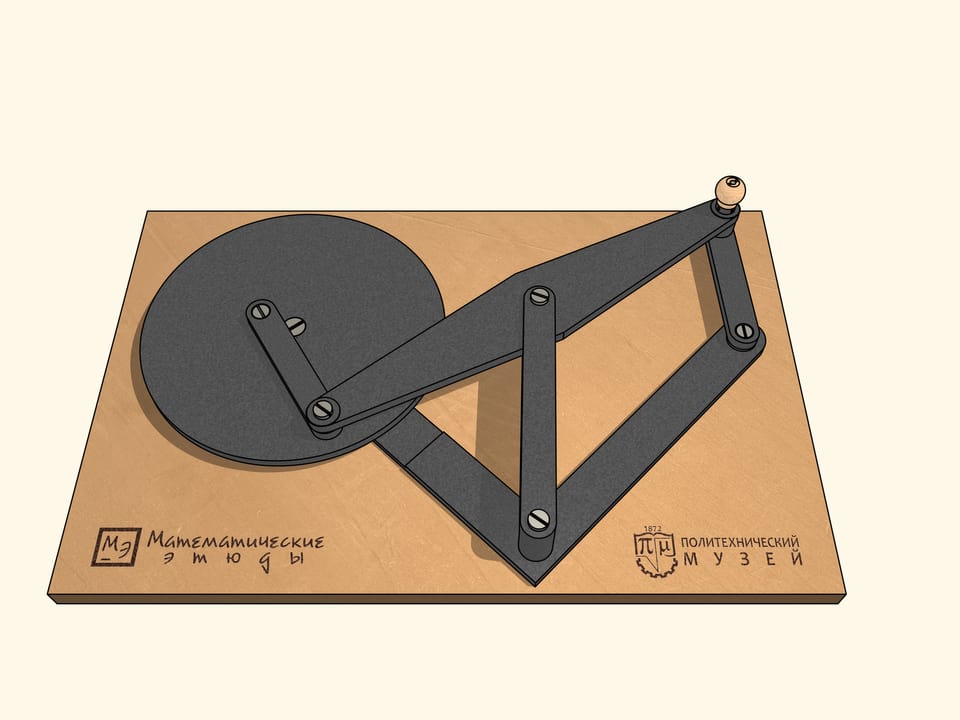
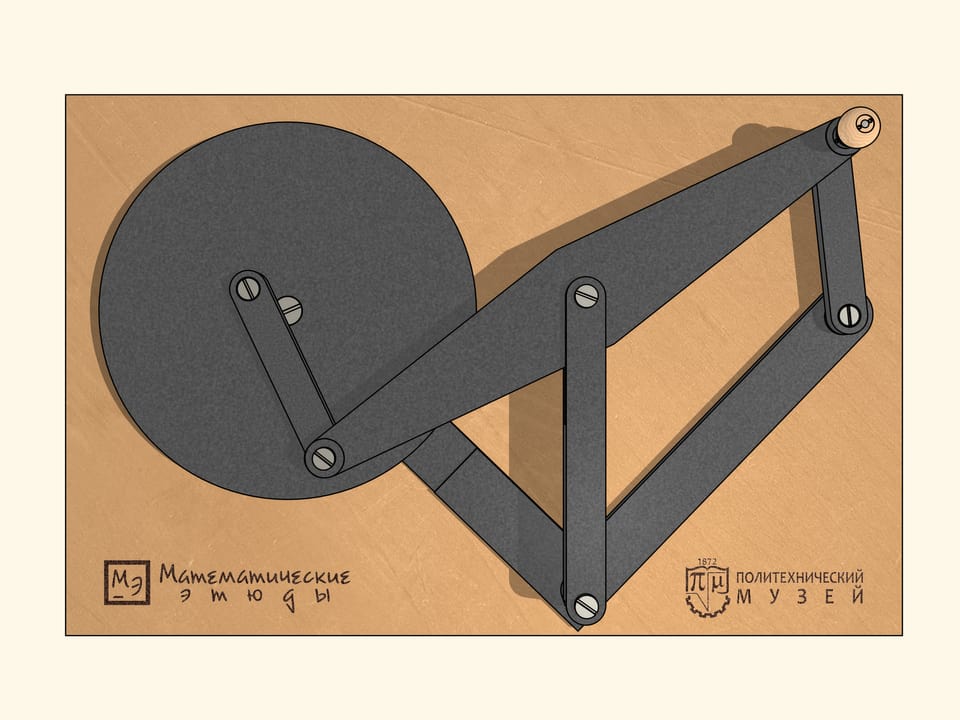
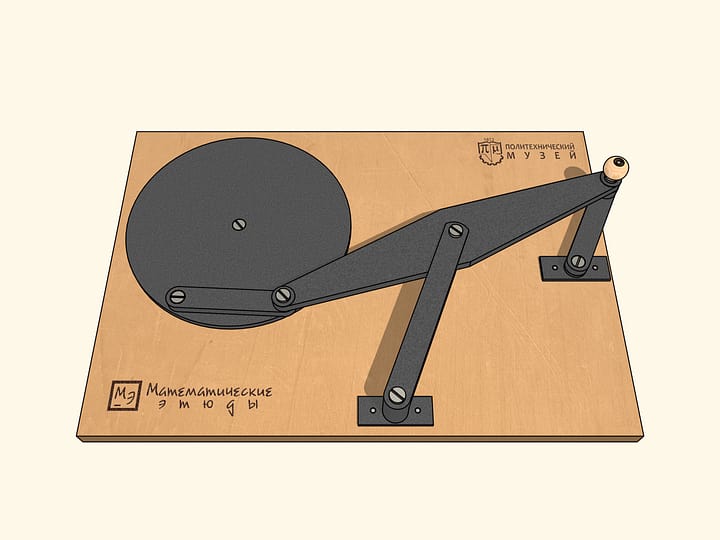
Con­sid­er­ing the case when the links form a line, we come up with a mech­a­nism that looks like the greek let­ter lambda. Tcheby­shev used it with some para­me­ters to build the first «tan­gent to two con­cen­tric cir­cles, remain­ing between them. By chang­ing the para­me­ters of the mech­a­nism, one can reduce the dis­tance between the con­cen­tric cir­cles, within which is the blue tra­jec­tory.

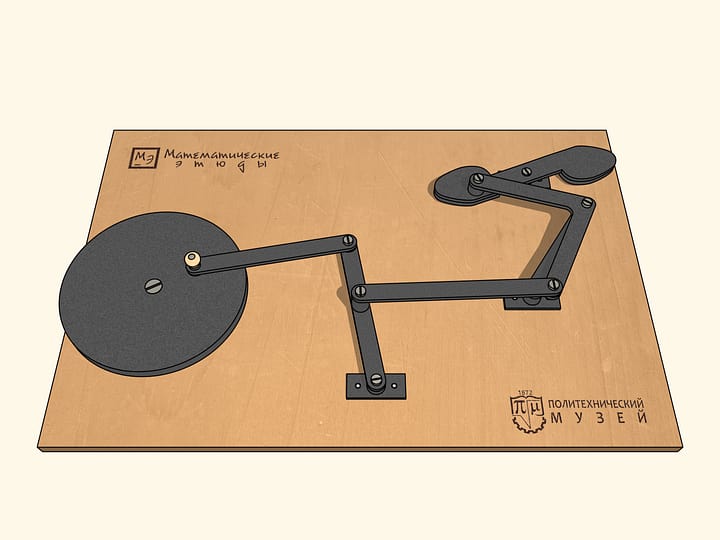
Improve the lambda-mech­a­nism by adding a fixed hinge and two links, whose sum of the lengths is equal to the radius of the larger cir­cle, and the dif­fer­ence: the radius of the smaller one.

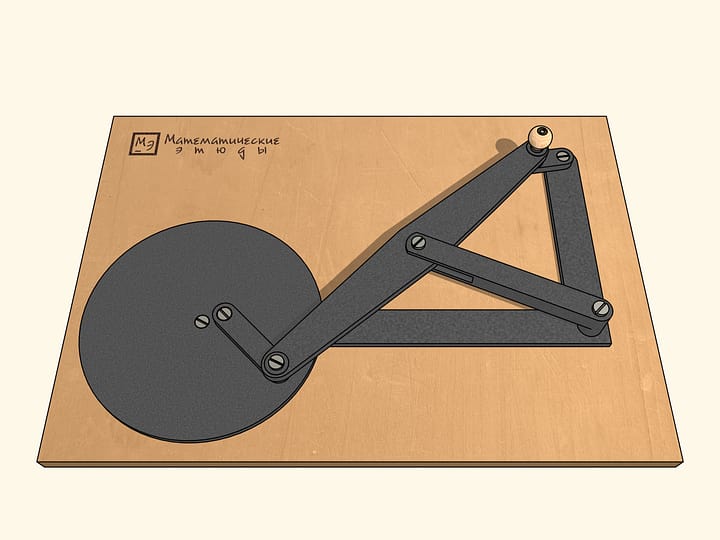
The mech­a­nism we get has bifur­ca­tion points, or as one says, sin­gu­lar points. Being in such a point dur­ing the same clock­wise motion of the lambda-mech­a­nism, the links may six­such bifur­ca­tion points: when the added links are on the same line.

There is a big and impor­tant brach of math­e­mat­ics, sin­gu­lar­ity the­ory, that stud­ies sin­gu­lar points. A very sim­ple and impor­tant case is the study of func­tion behav­ior through study­ing its points of max­i­mum and min­i­mum.

In order for our mech­a­nism to pass the six sin­gu­lar points in a pre­s­e­lected direc­tion, a small link is asso­ci­ated with a fly­wheel, which being pro­moted in some way, con­ducts the mech­a­nism from a sin­gu­lar point rotat­ing in the same direc­tion.

If one twists the fly­wheel, as well as the lead­ing link, clock­wise from the point of bifur­ca­tion, then in one turn of the lead­ing link the fly­wheel will do two turns.

If one twists the fly­wheel, coun­ter­clock­wise from the point of bifur­ca­tion, then in one clock­wise turn of the lead­ing link the fly­wheel will do four turns!

Therein lies the para­dox of this mech­a­nism, invented and made by Pafnuty Lvovich Tcheby­shev. It might seem that a flat hinge mech­a­nism must oper­ate unam­bigu­ously, how­ever, as we see, this is not always the case. And the rea­son is the sin­gu­lar point.